Tangram: Wie Sie das Legespiel im Geometrieunterricht einsetzen

Tangram-Vorlagen zum Download

Hier finden Sie einige Tangram-Vorlagen, die Sie kostenlos herunterladen und ausdrucken dürfen: Entweder als einzelne Bilder oder als gesammelte PDF mit allen Figuren und den dazugehörigen Lösungen.

Einzelne Tangram-Figuren:

Alle Tangram-Aufgaben inklusive Lösungen:

Was kann das Tangram?

Bei einem Tangram-Bild ist die „wirkliche“ Form stark abstrahiert. Das Bild entsteht erst im Kopf, denn unser Gehirn sucht nach Bekanntem und assoziiert Figürliches aus den abstrakten Formen. Gerade diese Assoziationsfähigkeit macht es so knifflig, hinter das Legemuster der Tangram-Figur zu kommen: Man sieht eine Ente, soll aber an Dreiecke und Quadrate denken.

Ein besonderer Knobeleffekt liegt darin, dass ein Bild meist mehr als eine Tangram-Lösung hat. Denn die größeren geometrischen Formen lassen sich aus verschiedenen kleineren zusammensetzen. Somit haben die Tans häufig keinen festgelegten Platz in der abgebildeten Figur.

5 Vorzüge des Tangrams in der Grundschule

Die Beschäftigung mit Tangram verbindet den Geometrieunterricht mit Rätselspaß. Hier werden keine Formeln gepaukt, sondern bildhafte Knobel-Aufgaben gelöst. Auf spielerische Weise schult das Tangram logisches Denken und trainiert die räumliche Vorstellung. Auch die Kreativität wird beim Finden von Tangram-Lösungen gefordert.

Deshalb ist Tangram in der Grundschule ein ideales Lehrmittel:
Die Kinder

• entwickeln grundlegendes Verständnis für Flächen,
• gewinnen Orientierung im zweidimensionalen Raum,
• werden mit den Bezeichnungen der Flächenformen vertraut,
• verstehen die Beziehungen geometrischer Formen und
• entwickeln geometrische Intuition.

Der Lernweg zum Tangram

Damit die Kinder Tangram-Figuren nachlegen können, müssen sie zunächst mit dem Material vertraut werden und Erfahrungen mit dem Nachlegen der Figuren machen. Anfangs legen sie deshalb originalgroße Vorlagen aus, wobei Hilfslinien die Position der Tans zeigen. So entwickeln sie schrittweise ihr Kombinationsgeschick.

Tangram-Karten für die Grundschule sollten sowohl Vorlagen als auch Legevorschläge enthalten.

Der Lernweg erfolgt schrittweise in 4 Schwierigkeitsstufen:
Schritt 1: Figuren in Originalgröße auslegen, mit Hilfslinien
Schritt 2: Figuren in Originalgröße auslegen, ohne Hilfslinien
Schritt 3: verkleinerte Figuren nachlegen, mit Hilfslinien
Schritt 4: verkleinerte Figuren nachlegen, ohne Hilfslinien

Das Tangram im Geometrieunterricht

Anfangs empfiehlt es sich, wichtige Punkte kurzgefasst auf einem Plakat im Klassenraum auszuhängen. Nach der Methode des Scaffolding dient das Lernplakat als Orientierungshilfe sowie zur Selbstkontrolle, bis die Kinder sicher genug sind, Personenbeschreibungen eigenständig zu verfassen.

Das Tangram lässt sich von der ersten Klasse bis in die Sekundarstufe einsetzen. So können die Aufgaben im Geometrieunterricht mit den geometrischen Grundfiguren des Tangrams immer wieder aufgegriffen und auf höherem Niveau vertieft werden. Das Tangram fördert sowohl inhalts- als auch prozessbezogene Kompetenzen.

Inhaltsbezogene Kompetenzen

Zu den wesentlichen Lehrplaninhalten im Kompetenzbereich „Umgang mit Raum und Form“ gehört das Untersuchen von ebenen Figuren, der Vergleich von Flächeninhalten sowie Erkennen und Nutzen von Symmetrie. Das Tangram eignet sich besonders gut, um diese Inhalte verständlich zu machen.

Wer ein Tangram-Puzzle löst, beschäftigt sich ganz von selbst mit Beziehungen unter Polygonen von verschiedener Form aber gleichem Flächeninhalt, mit Winkeln, Parallelen und Symmetrien. So lassen sich formale Sätze herleiten und veranschaulichen.

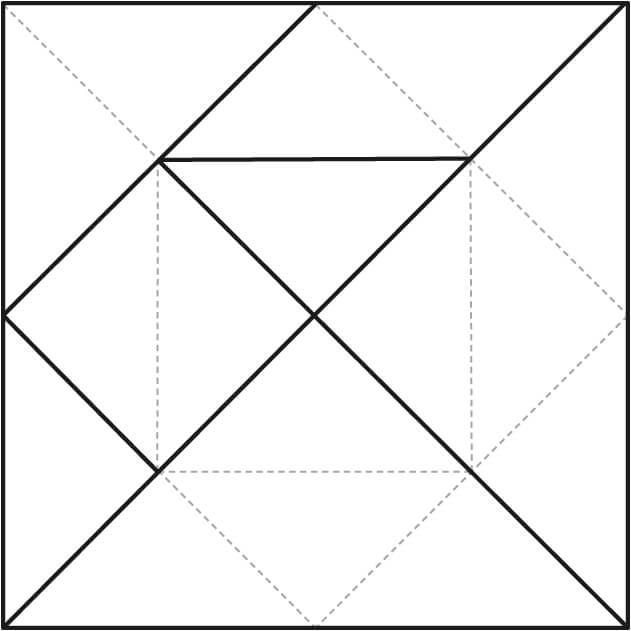
Diese Beobachtungen machen die Schüler im Tangram-Quadrat:

• Alle Tans können in gleichgroße rechtwinklige Dreiecke unterteilt werden.
• Die 7 Tans ergeben insgesamt 16 rechtwinklige Dreiecke.
• Die Fläche jedes Tans ist ein rationales Vielfaches des kleinen Dreiecks:
  • kleine Dreiecke mit Flächeninhalt 1
  • Quadrat, mittleres Dreieck und Parallelogramm mit Flächeninhalt 2
  • große Dreiecke mit Flächeninhalt 4
• Jeder Winkel ist ein Vielfaches des 45°-Winkels.
• Alle Formen mit Ausnahme des Parallelogramms sind achsensymmetrisch.

Prozessbezogene Kompetenzen

Durch das Hantieren und Probieren mit konkretem Material bewirkt das Tangram eine aktive Auseinandersetzung mit Geometrie – und so manchen Aha-Effekt. Das bezieht Kompetenzen ein, die zu einem gesicherten Verständnis mathematischer Inhalte entscheidend beitragen.

1. Die Fähigkeit zum kreativen Problemlösen wird angesprochen, wenn ein Umriss mit allen Tangram-Teilen ausgelegt werden soll, ohne dass eine Lösung auf der Hand liegt. Ziel des Tangram-Spiels ist es, eigene Lösungsstrategien zu entwickeln und auf ähnliche Situationen zu übertragen. Wie etwa beim Erfinden eigener Tangram-Figuren.

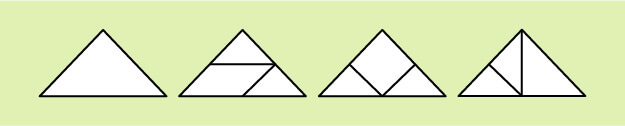
2. Unter Argumentieren versteht man, Vermutungen über mathematische Zusammenhänge anzustellen, einzelne Erfahrungen auf allgemeine Gültigkeit zu überprüfen und Gesetzmäßigkeiten zu erkennen. Eine Aufgabe beim Tangram kann beispielsweise sein: Wie viele Möglichkeiten gibt es, die Form des großen Dreiecks nachzulegen?

3. Zu der Kompetenz Darstellen, Kommunizieren gehört, dass die Schüler Aufgaben im Team lösen, Vorgehensweisen dokumentieren und Ergebnisse präsentieren. Hierbei üben sie auch fachsprachliche Begriffe ein. Eine Aufgabe kann lauten: Erfinde selbst eine Tangram-Vorlage und erstelle eine Anleitung, wie man die Tangram-Figur nachlegen kann.

Wie viele Möglichkeiten gibt es? Tangram fördert wichtige Kompetenzen im Geometrieunterricht

Das Tangram im Tandem

Üblicherweise wird Tangram von einem Spieler allein gespielt. Doch im Geometrieunterricht eignet es sich sehr gut für die Partnerarbeit. Das gemeinsame Knobeln fordert die Schüler auf, Legestrategien zu diskutieren und verschiedenen Tangram-Lösungen verbal zu begründen.

Diese Aktivitäten ermöglicht das Tangram in Partnerarbeit:

• Beschreiben, welche geometrische Figur gelegt werden soll.
  Ein Tandempartner gibt mündliche Anweisungen, die der andere mit dem Tangram ausführt.

• Eigene Tangram-Figuren aufzeichnen und austauschen.
  Die Schüler stellen sich gegenseitig Rätselaufgaben, indem sie ihre selbst erstellten Tangram-Vorlagen tauschen.

• Fehler in einer vorgegebenen Umrissfigur finden.
  Die Schüler erhalten eine fehlerhafte Tangram-Vorlage und sollen herausfinden, was nicht funktioniert. Die Frage nach Verbesserungsvorschlägen schult die Problemlösekompetenz.

• Möglichst viele Variationen finden, Zwillings-Tangrams zu legen.
  Ein Zwillings-Tangram besteht aus zwei kongruenten Figuren, die zusammen ein Tangram bilden. Insgesamt gibt es 60 Zwillings-Tangrams. Hier sind drei Beispiele:

Zwillings-Tangram: Jedes Paar wird aus den 7 Tangram-Spielsteinen gelegt.